leetcode-双指针相关题型

发表于 更新于 分类于 Changyan：
双指针相关题型

盛最多水的容器

给你 n 个非负整数 a1，a2，…，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器，且 n 的值至少为 2。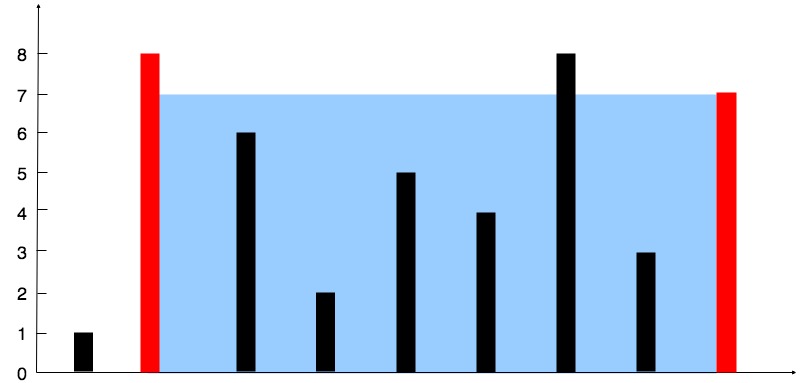

示例：
输入：[1,8,6,2,5,4,8,3,7]
输出：49

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int maxArea(vector<int>& height) {
        int len=height.size();
        if(len<2)
            return 0;
        int l=0;
        int r=len-1;
        int maxArea=0;
        while(l<r) {
            maxArea=max(maxArea, (r-l)*min(height[l], height[r]));
            if(height[l]<height[r])
                l++;
            else
                r--;
        }
        return maxArea;
    }
};

比较版本号

给你两个版本号 version1 和 version2 ，请你比较它们。

版本号由一个或多个修订号组成，各修订号由一个 ‘.’ 连接。每个修订号由 多位数字 组成，可能包含 前导零 。每个版本号至少包含一个字符。修订号从左到右编号，下标从 0 开始，最左边的修订号下标为 0 ，下一个修订号下标为 1 ，以此类推。例如，2.5.33 和 0.1 都是有效的版本号。

比较版本号时，请按从左到右的顺序依次比较它们的修订号。比较修订号时，只需比较 忽略任何前导零后的整数值 。也就是说，修订号 1 和修订号 001 相等 。如果版本号没有指定某个下标处的修订号，则该修订号视为 0 。例如，版本 1.0 小于版本 1.1 ，因为它们下标为 0 的修订号相同，而下标为 1 的修订号分别为 0 和 1 ，0 < 1 。

比较两个版本号大小，版本号由修订号组成，中间使用’.’分隔，越靠近字符串前边，修订号的优先级越大。当v1 > v2时返回 1，当v1 < v2时返回 -1，相等时返回 0

1
2
3
4
5
6
7
8
9
10
11
12
13
int compareVersion(string version1, string version2) {
    int i = 0, j = 0;
    while(i < version1.size() || j < version2.size())
    {
        long long num1 = 0, num2 = 0;   //数据加强了，这里要用long long
        while(i < version1.size() && version1[i] != '.') num1 = num1 * 10 + version1[i++] - '0';
        while(j < version2.size() && version2[j] != '.') num2 = num2 * 10 + version2[j++] - '0';
        if(num1 > num2) return 1;
        else if( num1 < num2) return -1;
        i++,j++;
    }
    return 0;
}

判断子序列

给定字符串 s 和 t ，判断 s 是否为 t 的子序列。
字符串的一个子序列是原始字符串删除一些（也可以不删除）字符而不改变剩余字符相对位置形成的新字符串。（例如，”ace”是”abcde”的一个子序列，而”aec”不是）。

我们从前往后匹配，可以发现每次贪心地匹配靠前的字符是最优决策。

1
2
3
4
5
6
7
8
9
10
11
bool isSubsequence(string s, string t) {
    int n = s.length(), m = t.length();
    int i = 0, j = 0;
    while (i < n && j < m) {
        if (s[i] == t[j]) {
            i++;
        }
        j++;
    }
    return i == n;
}

数组中最大数对和的最小值

一个数对 (a,b) 的 数对和 等于 a + b 。最大数对和 是一个数对数组中最大的 数对和 。

比方说，如果我们有数对 (1,5) ，(2,3) 和 (4,4)，最大数对和 为 max(1+5, 2+3, 4+4) = max(6, 5, 8) = 8 。
给你一个长度为 偶数 n 的数组 nums ，请你将 nums 中的元素分成 n / 2 个数对，使得：

  • nums 中每个元素 恰好 在 一个 数对中，且
  • 最大数对和 的值 最小 。
    请你在最优数对划分的方案下，返回最小的 最大数对和

本题用自然智慧（未严格证明）不难想到这样的贪心策略
船的吨位规格只取决于体重和最大的那一对，如果最大这一对满足了，其他人都可以满足。
最优的搭配方案应该是，最后使得每一对（体重和）之间尽可能的接近，即各队尽可能平均，我们不希望队与队之间差别较大。
考虑最大体重的那个人，谁跟他搭配可以使得体重和最优？是最轻的那个（如果是跟其他人组队，会使得这一对的体重和较大，最终可能不够平均）
我们先满足他俩，剩下的人又是一个相同的子问题了。

1
2
3
4
5
6
7
public static int minPairSum(int[] nums) {
    Arrays.sort(nums);
    int n = nums.length, l = 0, r = n-1, maxSum = Integer.MIN_VALUE;
    while (l < r)
        maxSum = Math.max(maxSum, nums[l++]+nums[r--]);
    return maxSum;
}

总结

类似这种求最大值的题型，如果采用暴力求解法，时间复杂度：O(n2)，需要把所有情况都考虑到，而采用这种两边往中间逼近的双指针法，就可以只需遍历一次就能找到最大值，需要弄明白什么时候左边逼近，什么时候右边逼近，以及左边永远不能大于右边(l<r)，当碰到这种一次遍历就要找到最值的问题，优先考虑双指针逼近法。