stl组成部分
容器、算法、迭代器、仿函数(函数对象),比如比较器、适配器、空间适配器(内存分配器)
容器
C++ 提供了多种标准容器。以下是 C++ 中常见的容器:
Array:静态数组,大小固定。
Vector:动态数组,支持随机访问和动态扩容。
List:双向链表,支持插入和删除操作。
Forward_list:单向链表,支持插入和删除操作。
Deque:双端队列,支持在队首和队尾进行插入和删除操作。
Stack:栈,支持基本的栈操作,先进后出。
Queue:队列,支持基本的队列操作,先进先出。
PriorityQueue:优先队列,支持按优先级插入和删除元素。
Set:集合,不允许重复元素,元素按一定的排序规则存储。
Map:映射,不允许重复的 key,元素按 key 的大小排序存储。
Unordered_set:哈希表实现的集合,不允许重复元素。
Unordered_map:哈希表实现的映射,不允许重复的 key。
迭代器的实现原理
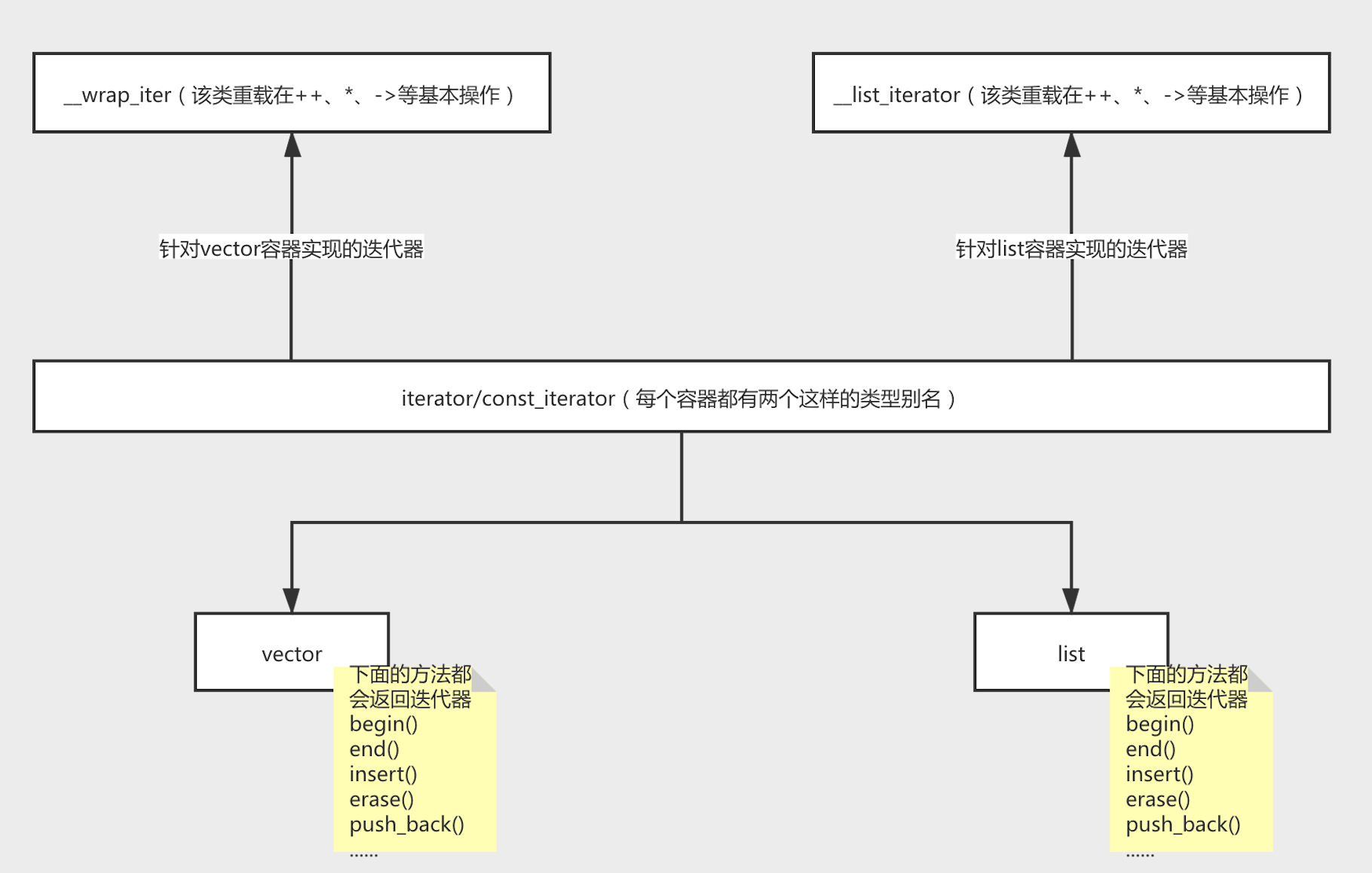
从上图中可以看出,STL通过类型别名的方式实现了对外统一;在不同的容器中类型别名的真实迭代器类型是不一样的,而且真实迭代器类型对于++、–、*、->等基本操作的实现方式也是不同的。(PS:迭代器很好地诠释了接口与实现分离的意义)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
|
#ifndef CPP_PRIMER_MY_LIST_H
#define CPP_PRIMER_MY_LIST_H
#include <iostream>
template<typename T>
class node {
public:
T value;
node *next;
node() : next(nullptr) {}
node(T val, node *p = nullptr) : value(val), next(p) {}
};
template<typename T>
class my_list {
private:
node<T> *head;
node<T> *tail;
int size;
private:
class list_iterator {
private:
node<T> *ptr;
public:
list_iterator(node<T> *p = nullptr) : ptr(p) {}
T &operator*() const {
return ptr->value;
}
node<T> *operator->() const {
return ptr;
}
list_iterator &operator++() {
ptr = ptr->next;
return *this;
}
list_iterator operator++(int) {
node<T> *tmp = ptr;
++(*this);
return list_iterator(tmp);
}
bool operator==(const list_iterator &t) const {
return t.ptr == this->ptr;
}
bool operator!=(const list_iterator &t) const {
return t.ptr != this->ptr;
}
};
public:
typedef list_iterator iterator;
my_list() {
head = nullptr;
tail = nullptr;
size = 0;
}
void push_back(const T &value) {
if (head == nullptr) {
head = new node<T>(value);
tail = head;
} else {
tail->next = new node<T>(value);
tail = tail->next;
}
size++;
}
void print(std::ostream &os = std::cout) const {
for (node<T> *ptr = head; ptr != tail->next; ptr = ptr->next)
os << ptr->value << std::endl;
}
public:
iterator begin() const {
return list_iterator(head);
}
iterator end() const {
return list_iterator(tail->next);
}
};
#endif
|
迭代器失效
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
#include <iostream>
#include <vector>
int main ()
{
std::vector<int> myvector (3,100);
std::vector<int>::iterator it;
it = myvector.begin();
it = myvector.insert ( it , 200 );
myvector.insert (it,200,300);
myvector.insert (it,5,500);
for (std::vector<int>::iterator it2=myvector.begin(); it2<myvector.end(); it2++)
std::cout << ' ' << *it2;
std::cout << '\n';
return 0;
}
|
当执行完myvector.insert (it,200,300);这条语句后,实际上myvector已经申请了一块新的内存空间来存放之前已保存的数据和本次要插入的数据,由于it迭代器内部的指针还是指向旧内存空间的元素,一旦旧内存空间被释放,当执行myvector.insert (it,5,500);时就会crash(PS:因为你通过iterator的指针正在操作一块已经被释放的内存,大多数情况下都会crash)。迭代器失效就是指:迭代器内部的指针没有及时更新,依然指向旧内存空间的元素。
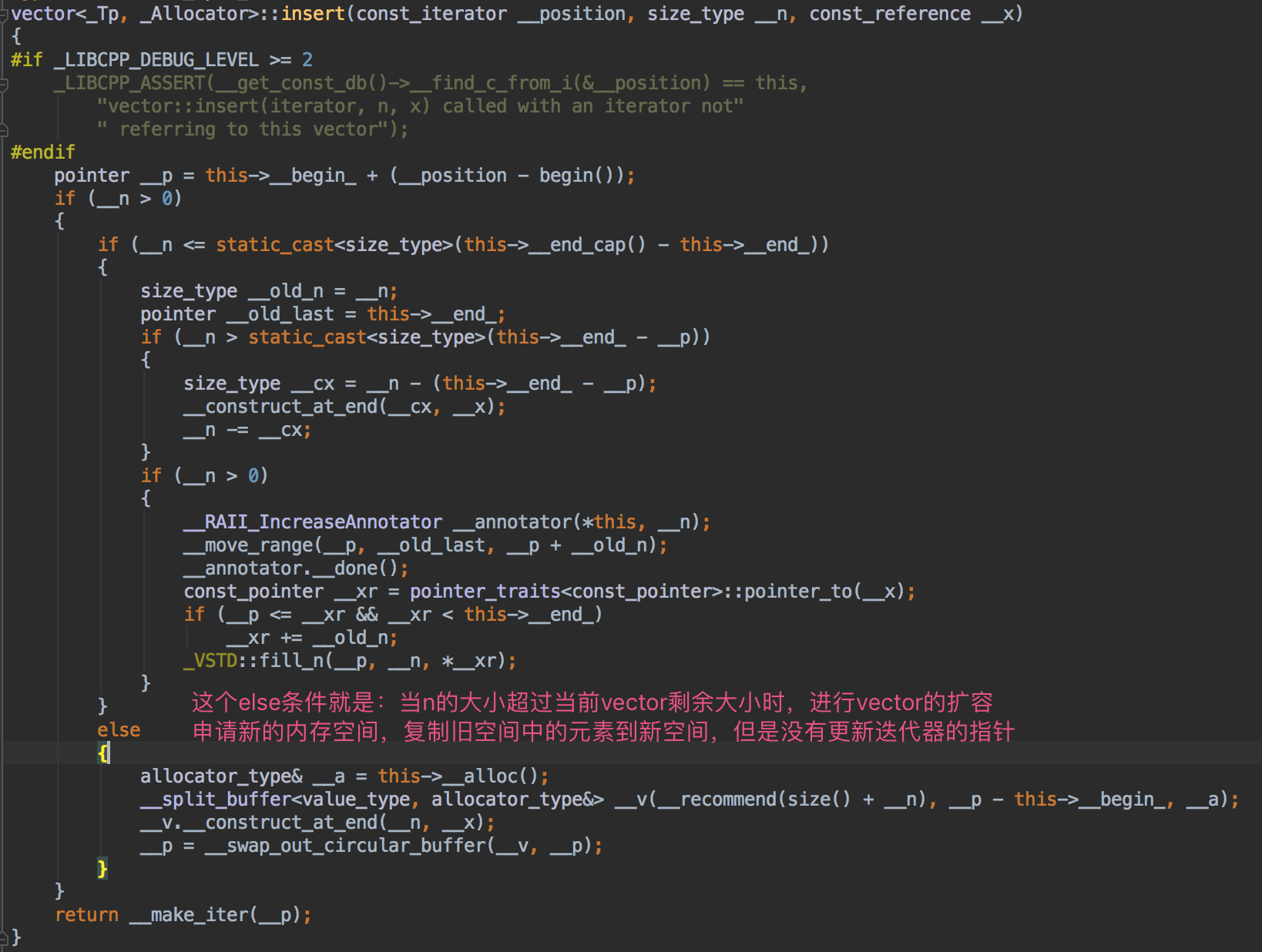
上图展示了STL源码中vector容器insert方法的实现方式。当插入的元素个数超过当前容器的剩余容量时,就会导致迭代器失效。这也是测试代码中myvector.insert (it,200,300);插入200个元素的原因,为了模拟超过当前容器剩余容量的场景,如果你的测试环境没有crash,可以将插入元素设置的更多一些。
Vector与Array的区别?
- vector属于变长容器,即可以根据数据的插入删除重新构建容器容量;但array和数组属于定长容量。
- array提供了初始化所有成员的方法fill。
- 由于vector的动态内存变化的机制,在插入和删除时,需要考虑迭代的是否失效的问题。为了减少扩容操作的次数,可以在建立 vector 时尽可能地估计需要存储的元素数量,这样可以避免不必要的内存分配和拷贝操作,提高 vector 的性能和效率。
红黑树
红黑树是平衡二叉搜索(中序遍历有序)树,(avl是完全平衡,节点高度最大相差1),红黑树是平衡黑节点的高度,每条链路的黑节点个数是一样的,时间复杂度位O(logn),100w个节点比较20次,10亿个节点比较30次。
先插入,插入的都是红色节点,插入后检测规则重新着色或者平衡。
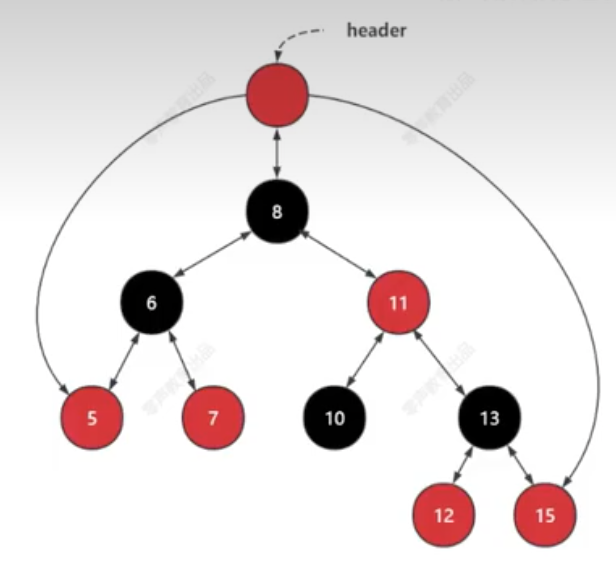
红黑树和AVL树都是平衡二叉搜索树,它们都具有自平衡的特点。但是,相比较而言,红黑树在插入和删除操作时的平衡调整次数是少于AVL树的,因此在实际应用中,红黑树比AVL树使用更为广泛。
主要原因有以下方面:
- AVL树是严格平衡的:每个节点的左右子树的高度相差不超过1。但是,为了维护这种严格的平衡性,当进行插入和删除操作时,可能需要对树进行多次旋转,使节点重新调整平衡。而红黑树通过允许节点的左右子树高度相差最多为2,而不纯粹为1,来减少平衡调整的次数。
- 红黑树执行的旋转更少:AVL树通常需要多次旋转,在一些场景中可能会导致较高的磁盘I/O,而红黑树更少的旋转意味着更少的指令,更少的代码缓存行等。
- 红黑树的颜色标记代替了 AVL 树的高度:红黑树通过结点着色来区分每个结点对整棵树的平衡性的贡献是多大,从而避免了AVL树中频繁的计算平衡因子,提高了插入和删除操作时的效率。
stl红黑树特征:
- O(1)的方式找到最大和最小节点,header节点是红色节点,连接最大值和最小值。
- 提供了key相同的处理方案,基于上图插入7号节点,将会放在原7号节点的右边。
- 提供了一个带提示的插入功能insert_hint,以最小的代价插入17号节点:最后一个节点是最小的。
如果key是string,比较长的话,考虑使用unordered_map,时间复杂度为O(1).
定时器方案优化,expire是一个固定值 1
2
3
4
5
6
7
8
9
| TimerNodeBase AddTimer(time_t msec, TimerNode::Callback func) {
time_t expire = GetTick() + msec;
if (timeouts.empty() || expire <= timeouts.crbegin()->expire) {
auto pairs = timeouts.emplace(GenID(), expire, std::move(func));
return static_cast<TimerNodeBase>(*pairs.first);
}
auto ele = timeouts.emplace_hint(timeouts.crbegin().base(), GenID(), expire, std::move(func));
return static_cast<TimerNodeBase>(*ele);
}
|
map和set:
1
2
3
4
5
6
7
8
9
10
11
|
template <class _Key, class _Compare = less<_Key>,
class _Allocator = allocator<_Key> >
typedef _Rb_tree<key_type, value_type, _Identity<value_type>,
key_compare, _Key_alloc_type> _Rep_type;
template <class _Key, class _Tp, class _Compare = less<_Key>,
class _Allocator = allocator<pair<const _Key, _Tp> > >
typedef _Rb_tree<key_type, value_type, _Select1st<value_type>,
key_compare, _Pair_alloc_type> _Rep_type;
|
map和multimap:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
std::pair<iterator, bool> insert(const value_type& __x)
{
return _M_t._M_insert_unique(__x);
}
iterator insert(const value_type& __x)
{
return _M_t._M_insert_equal(__x);
}
_M_get_insert_equal_pos(const key_type& __k)
{
typedef pair<_Base_ptr, _Base_ptr> _Res;
_Link_type __x = _M_begin();
_Base_ptr __y = _M_end();
while (__x != 0)
{
__y = __x;
__x = _M_impl._M_key_compare(__k, _S_key(__x)) ? _S_left(__x) : _S_right(__x);
}
return _Res(__x, __y);
}
|
二叉搜索树的下一个节点?
- 某个节点有右子树,就找右子树的最左侧的节点。8号节点。
- 没有右子树
a. 该节点是父节点的左子树,后继节点就是父节点,5号节点。
b. 该节点是父节点的右子树,沿着父节点去查找,将问题转化为a,7号节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| static _Rb_tree_node_base *
local_Rb_tree_increment( _Rb_tree_node_base* __x ) throw ()
{
if ( __x->_M_right != 0 )
{
__x = __x->_M_right;
while ( __x->_M_left != 0 )
__x = __x->_M_left;
} else {
_Rb_tree_node_base *__y = __x->_M_parent;
while ( __x == __y->_M_right )
{
__x = __y;
__y = __y->_M_parent;
}
if ( __x->_M_right != __y )
__x = __y;
}
return (__x);
}
|



