leetcode-单调栈题型

发表于 更新于 Changyan：

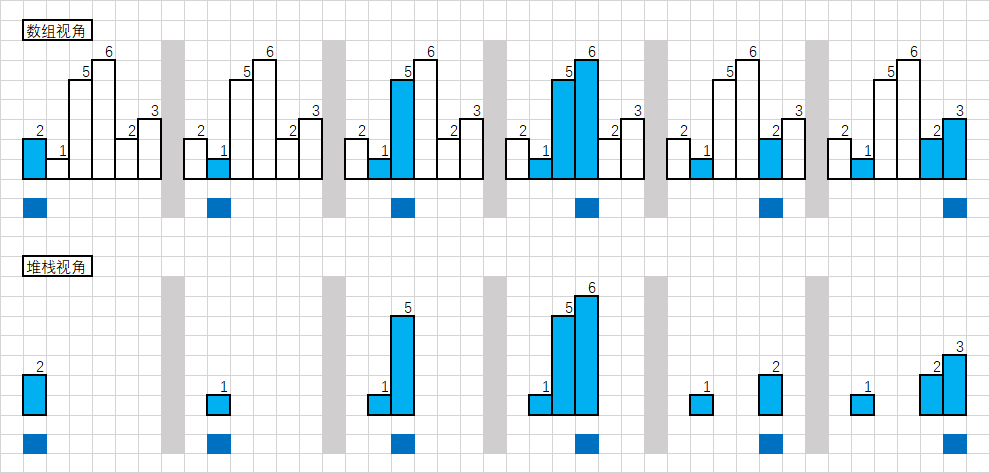
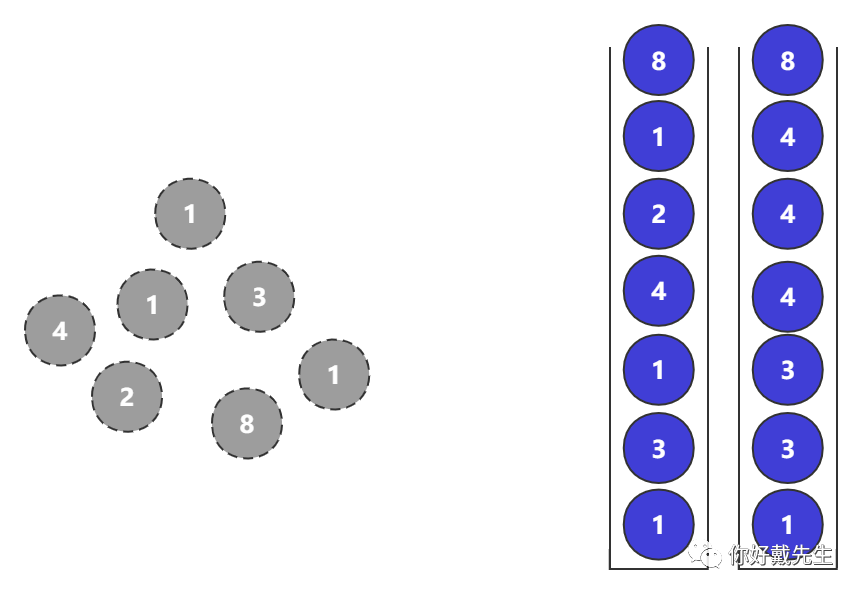
单调栈分为单调递增栈和单调递减栈

  1. 单调递增栈即栈内元素保持单调递增的栈
  2. 同理单调递减栈即栈内元素保持单调递减的栈
    操作规则（下面都以单调递增栈为例）
  3. 如果新的元素比栈顶元素大，就入栈
  4. 如果新的元素较小，那就一直把栈内元素弹出来，直到栈顶比新元素小

柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。
求在该柱状图中，能够勾勒出来的矩形的最大面积。

1
2
3
4
5
6
7
8
9
stack<int> st;
for(int i = 0; i < nums.size(); i++)
{
	while(!st.empty() && st.top() > nums[i])
	{
		st.pop();
	}
	st.push(nums[i]);
}

对于一个高度，如果能得到向左和向右的边界
那么就能对每个高度求一次面积
遍历所有高度，即可得出最大面积
使用单调栈，在出栈操作时得到前后边界并计算面积

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
int largestRectangleArea(vector<int>& heights)
{
    int ans = 0;
    vector<int> st;
    heights.insert(heights.begin(), 0);
    heights.push_back(0);
    for (int i = 0; i < heights.size(); i++)
    {
        while (!st.empty() && heights[st.back()] > heights[i]) // 大的都弹出去
        {
            int cur = st.back();
            st.pop_back();
            int left = st.back() + 1;
            int right = i - 1;
            ans = max(ans, (right - left + 1) * heights[cur]);
        }
        st.push_back(i);
    }
    return ans;
}

滑动窗口最大值

给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回 滑动窗口中的最大值 。

1
2
3
4
5
6
7
8
9
10
11
输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]
解释：
滑动窗口的位置                最大值
---------------               -----
[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

遍历数组，将 数 存放在双向队列中，并用 L,R 来标记窗口的左边界和右边界。队列中保存的并不是真的 数，而是该数值对应的数组下标位置，并且数组中的数要从大到小排序。如果当前遍历的数比队尾的值大，则需要弹出队尾值，直到队列重新满足从大到小的要求。刚开始遍历时，L 和 R 都为 0，有一个形成窗口的过程，此过程没有最大值，L 不动，R 向右移。当窗口大小形成时，L 和 R 一起向右移，每次移动时，判断队首的值的数组下标是否在 [L,R] 中，如果不在则需要弹出队首的值，当前窗口的最大值即为队首的数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
    //使用双向队列。
    vector<int> res;
    deque<int> dq;
    for (int i = 0; i < nums.size(); ++i) {
        //如果窗口长度已经超过了k，则将最左边的元素移除
        if (!dq.empty() && dq.front() == i - k) dq.pop_front();
        //从后往前移除所有队列中小于当前元素的元素
        while (!dq.empty() && nums[i] > nums[dq.back()]) dq.pop_back();
        //在队列中添加当前元素
        dq.push_back(i);
        //如果窗口长度已经到达了k，则在结果中插入最大值(deque最前面的元素)
        if (i >= k-1) res.push_back(nums[dq.front()]);
    }
    return res;
}

实现最大（小）栈

实现一个最大（小）栈，即可随时拿出当前栈中最大（小）的元素

比较简单的办法就是使用两个栈来实现这个特殊的栈
其中一个栈stack正常进出元素
另外一个栈stackMax（stackMin）在进元素的时候，与栈顶的元素做一个比较
如果大于（小于）栈顶元素，则正常入栈
如果小于（大于）栈顶元素，则将当前栈顶的元素再次入栈

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class MaxHeap {
    stack<int> stack;
    stack<int> stackMax;

    int peekMax() {
        return stackMax.top();
    }

    int push(int item) {
        if (stack.empty()) {
            stackMax.push(item);
        } else {
            if (item > stackMax.top()) {
                stackMax.push(item);
            } else {
                stackMax.push(stackMax.top());
            }
        }
        stack.push(item);
        return item;
    }

    int peek() {
        return stack.top();
    }

    int pop() {
        stackMax.pop();
        return stack.pop();
    }
}