深度优先搜索和动态规划

算法和数据结构

解题思路：画图、推演、分解。代码编写：代码规范、功能正确、边界问题、异常处理、效率问题。

深度优先搜索

求可能解的问题，而广度优先搜索是求最优解的问题。
解题步骤：按照规则顺序搜索，尽量不重复不遗漏枚举出所有可能分支。使用递归来实现：使用栈、考虑好退出条件、自己调用自己，拆分出类似解。回溯：切换其他可能分支，注意恢复原状态。剪枝：优化搜索性能，去除重复解，发现找不到解可以提前退出。

例子：求一个字符串的所有排列组合，不含重复解，字符串长度小于8。
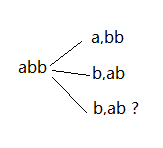
画递归树：先确定第一个字符，让后面的字符串bc作为一个整体，再让第一个字符a与后面的字符bc分别进行交换，里面的整体bc重复同样的操作。

void dfs(string &s, vector<string> &ans, int pos) {
    if (pos == s.size() - 1) { // pos从0开始，到最后一位的时候，不需要交换了
        ans.push_back(s); // s已经交换过了，就是其中的一个解
        return;
    }
    unordered_set<char> st;
    for (int i = pos; i < s.size(); i++) {
        if (st.find(s[pos]) != st.end()) { // 消除重复解，剪枝，提前退出
            continue;
        }
        if (i == pos) {
            dfs(s, ans, pos + 1); // 第一次不交换
            continue;
        }
        std::swap(s[i], s[pos]); // [0]和[1]交换、[0]和[2]交换，交换size()-1次
        dfs(s, ans, pos + 1);
        std::swap(s[i], s[pos]); // 回溯恢复状态
    }
}

例子：给定一个数字，按照规则翻译成字符串：0翻译成a，1翻译成b，…，25翻译成z，求0～2^31的数字能多少种翻译方法。

f(12258) = g(8)f(1225) + g(58)f(122)，g()判断能不能被翻译，g(8)=1, g(58)=0
画递归树：

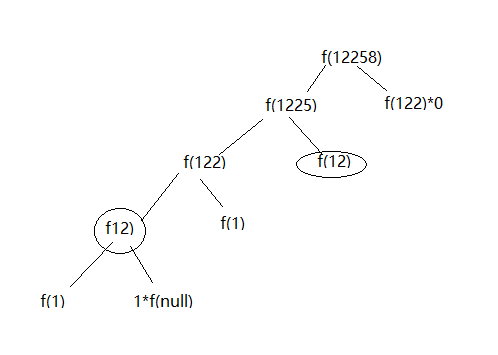
递归调用流程为：f(12258) -> f(1225) -> f(122) -> f(12) -> f(1) -> f(12) -> 1*f(null) -> f(122) -> f(1) -> f(122) -> f(1225) -> f(12) -> f(1225) ->f(12258)，类似于中序遍历。

int do(int num) {
    if (num < 10) return 1;
    int target = num % 100;
    if (tartget > 9 && target < 26) { // 这里相当于g()函数
        return do(num/10) + do(num/100);
    }
    return do(num/10);
}

// 优化版
int do2(int num) {
    unordered_map<int, int> cache;
    return dfs(num, cache);
}

int dfs(int num, unordered_map<int, int>&cache) {
    if (num < 10) return 1;
    if (cache.find(num) != cache.end()) {
        return cache[num]; // 之前已经有的解，就不要重复递归了
    }
    int target = num % 100;
    if (target > 9 && target < 26) {
        cache[num] = dfs(num/10, cache) + dfs(num/100, cache);
        return cache[num];
    }
    cache[num] = dfs(num/10, cache);
    return cache[num];
}

深度优先搜索是自顶向下的（递归的思路），而动态规划是自底向上的，是一种递推的解题思路，都需要对问题进行拆分，但动态规划的子问题的解是有重叠的，不是相互独立的。
解题步骤：拆分子问题，看子问题是否有重叠（某个节点的解是其父节点的一部分）。自底向上解决，确定边界，写出状态转移方程，dp记录子问题的解，减少重复计算。
递推公式：f(n) = f(n-1) + g(x)f(n-2) => f(n-1) = f(n-2) + g(x)f(n-3) f(n-1)是f(n)解的一部分
f(0)=1;
f(1)=1;
f(2)=f(1)+0f(0)=1,g(58)=0;
f(3)=f(2)+1f(1)=2,g(25)=1;
f(4)=f(3)+1f(2)=3,g(22)=1;
f(5)=f(4)+1f(3)=5,g(12)=1;

int do3(int num) {
    if (num < 10) return 1;
    int len = 1;
    for (int i = num; i > 10; i /= 10) {
        len++;
    }
    vector<int> dp(len+1);
    // 可以用滚动数组进行优化
    dp[0] = 1, dp[1] = 1;
    for (int i = 2; num > 10; num /= 10; i++) { // 需要算len次
        int target = num % 100;
        if (target > 9 && target < 26) {
            dp[i] = dp[i-1] + dp[i-2];
        else
            dp[i] = dp[i-1];
        }
    }
    return dp[len];
}