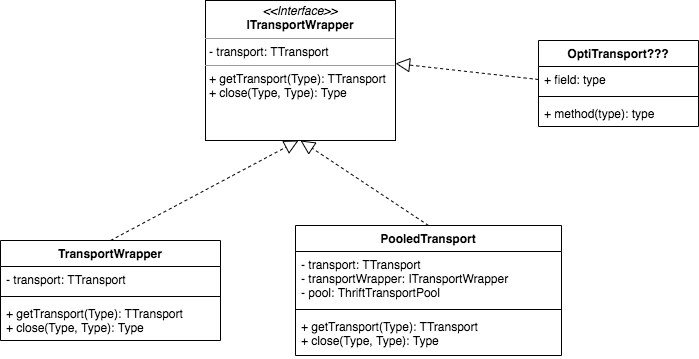
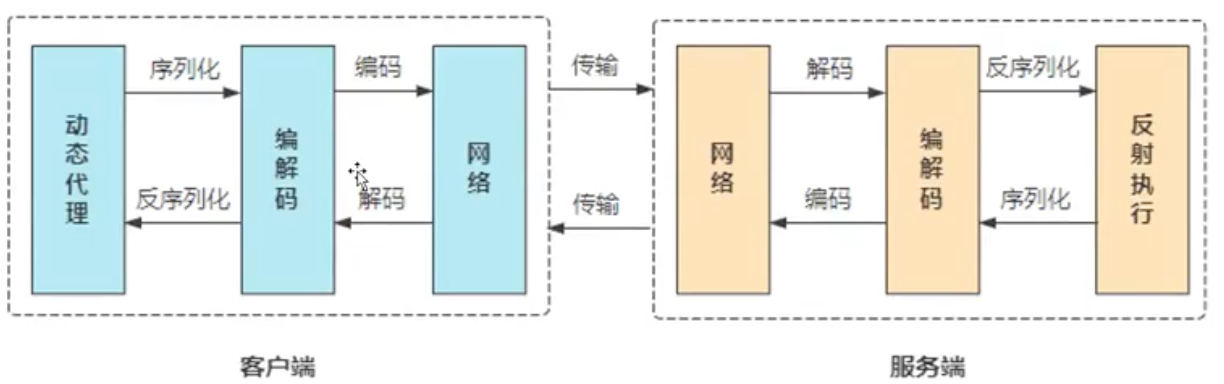
基于装饰者模式的thrift连接池实现(C++版本)
就一个连接池而已,为什么要采用装饰者模式,听着咋感觉那么高深?
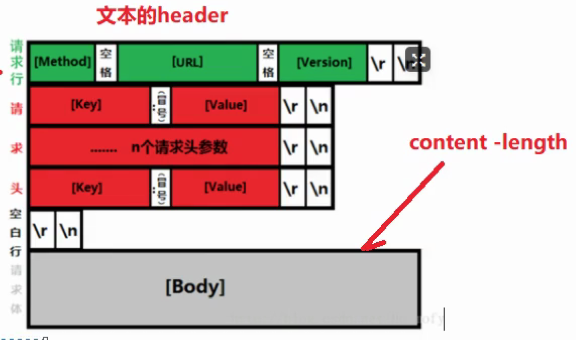
所谓连接池,也就是连接先不close,放入池中,等待下次需要用的时候,直接从池中取出即可用,省去了tcp握手的时间,所以这个可以看作是一个长连接,知道连接池清除空闲连接把多余的连接清除掉才会释放。
而普通的连接,用完后如果生命周期内不再使用了,就会销毁掉。
所以基于普通的连接,要定义出线程池的那种用完放回线程池的连接,就需要把close的方法进行重写,所以可以采用继承的方法实现,相当于产生了两个子类,一个是普通连接类,一个是线程池化的连接类。