二叉树相关算法题

发表于 | 更新于: | | 本文被围观了 次

如果中序遍历为有序的话则为二叉搜索树，为了避免退化为单链表，加入平衡规则后保持平衡则为平衡二叉树，搜索的时间复杂度为O(lgn).
满二叉树、完全二叉树又推出最大堆、最小堆（堆排序、定时器）。平衡二叉树又推出avl、红黑树。
对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。

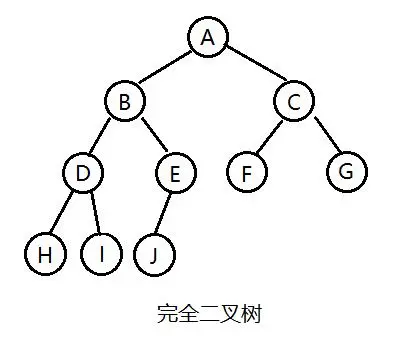
二叉树的递归遍历


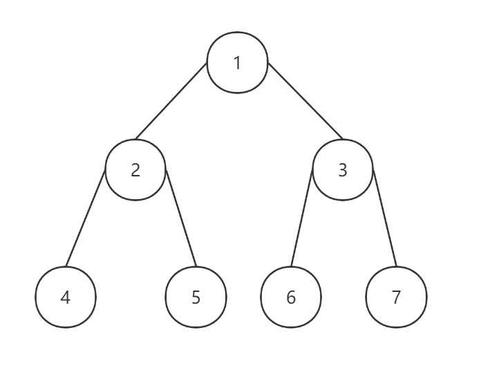
前序遍历：根->左->右，1>2>4>5>3>6>7，245这棵树是作为一个整体子树从根节点遍历，这就是递归的思想。
中序遍历：左->根->右，4>2>5>1>6>3>7，每次遍历到子树也是重新左->根->右进行遍历。
后序遍历：左->右->根，4>5>2>6>7>3>1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
void PreOrder(TreeNode *root)
{
    if (root == nullptr) return;
    result.push_back(root->val);
    PreOrder(root->left);
    PreOrder(root->right);
}

void InOrder(TreeNode *root)
{
    if (root == nullptr) return;
    InOrder(root->left);
    result.push_back(root->val);
    InOrder(root->right);
}

void PostOrder(TreeNode *root)
{
    if (root == nullptr) return;
    PostOrder(root->left);
    PostOrder(root->right);
    result.push_back(root->val);
}

二叉树的迭代遍历

栈是先进后出，前序遍历：根->左->右，1>2>4>5>3>6>7，所以要从右边往左进行压栈，顺序为右->左->根，思维方式恰好相反。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
void PreOrder(TreeNode *root)
{
    if (root == nullptr) return;
    stack<TreeNode*> st;
    st.push(root); // 先入根节点
    while (!st.empty()) {
        // 右->左->根
        TreeNode* node = st.top(); st.pop();
        if (node != nullptr) {
            if (node->right != nullptr) st.push(node->right);
            if (node->left != nullptr) st.push(node->left);
            st.push(node);
            st.push(nullptr); // 标记后面就是根节点
        } else { // 遇到标记才打印根节点
            node = st.top(); st.pop();
            result.push_back(node->val);
        }
    }
}

void InOrder(TreeNode *root)
{
    if (root == nullptr) return;
    stack<TreeNode*> st;
    st.push(root);
    while (!st.empty()) {
        // 右->根->左
        TreeNode* node = st.top(); st.pop();
        if (node != nullptr) {
            if (node->right != nullptr) st.push(node->right);
            st.push(node);
            st.push(nullptr); // 标记后面就是根节点
            if (node->left != nullptr) st.push(node->left);
        } else { // 遇到标记才打印根节点
            node = st.top(); st.pop();
            result.push_back(node->val);
        }
    }
}

void PostOrder(TreeNode *root)
{
    if (root == nullptr) return;
    stack<TreeNode*> st;
    st.push(root);
    while (!st.empty()) {
        // 根->右->左
        TreeNode* node = st.top(); st.pop();
        if (node != nullptr) {
            st.push(node);
            st.push(nullptr); // 标记后面就是根节点
            if (node->right != nullptr) st.push(node->right);
            if (node->left != nullptr) st.push(node->left);
        } else { // 遇到标记才打印根节点
            node = st.top(); st.pop();
            result.push_back(node->val);
        }
    }
}

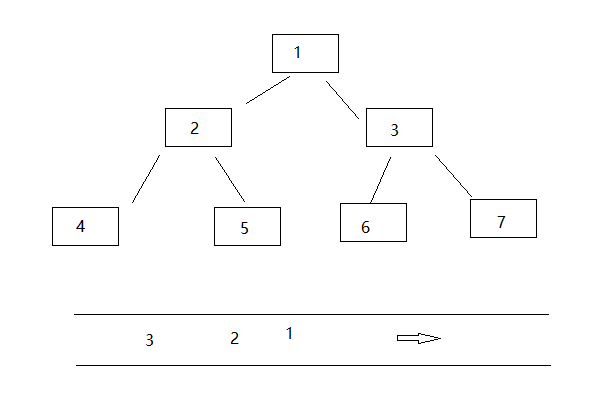
二叉树的层序遍历

广度优先搜索，需要使用队列来实现，和迭代类似，也是要让根节点先入，根节点弹出队列前，要把左右子节点入队列。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
vector<int> traverse(TreeNode *root)
{
    vector<int> result;
    if (root == nullptr) return result;
    queue<TreeNode*> que;
    que.push(root);
    while (!que.empty()) {
        size_t size = que.size();
        for (size_t i = 0; i < size; i++) { // 这里可以不写，但要知道它的存在
            TreeNode *node = que.front(); que.pop();
            result.push_back(node->val);
            if (node->left != nullptr) que.push(node->left); // 取出来后要将左右节点放进去
            if (node->right != nullptr) que.push(node->right);
        }
    }
}

// 按层打印
vector<vector<int>> traverse(TreeNode *root)
{
    vector<vector<int>> result;
    if (root == nullptr) return result;
    queue<TreeNode*> que;
    que.push(root);
    while (!que.empty()) {
        size_t size = que.size();
        vector<int> res;
        for (size_t i = 0; i < size; i++) { // 记录这一层有多少个节点
            TreeNode *node = que.front(); que.pop();
            res.push_back(node->val);
            if (node->left != nullptr) que.push(node->left); // 取出来后要将左右节点放进去
            if (node->right != nullptr) que.push(node->right);
        }
        result.push_back(res);
    }
}

二叉树树形dp

求最优解问题、且子问题的解有重叠（某个节点的解是其父节点的一部分），需要找到状态转移方程。
从二叉树的节点A出发，可以向上或向下走，但沿途的节点只能经过一次，当达到节点B时，路径上的节点树叫做A到B到距离。

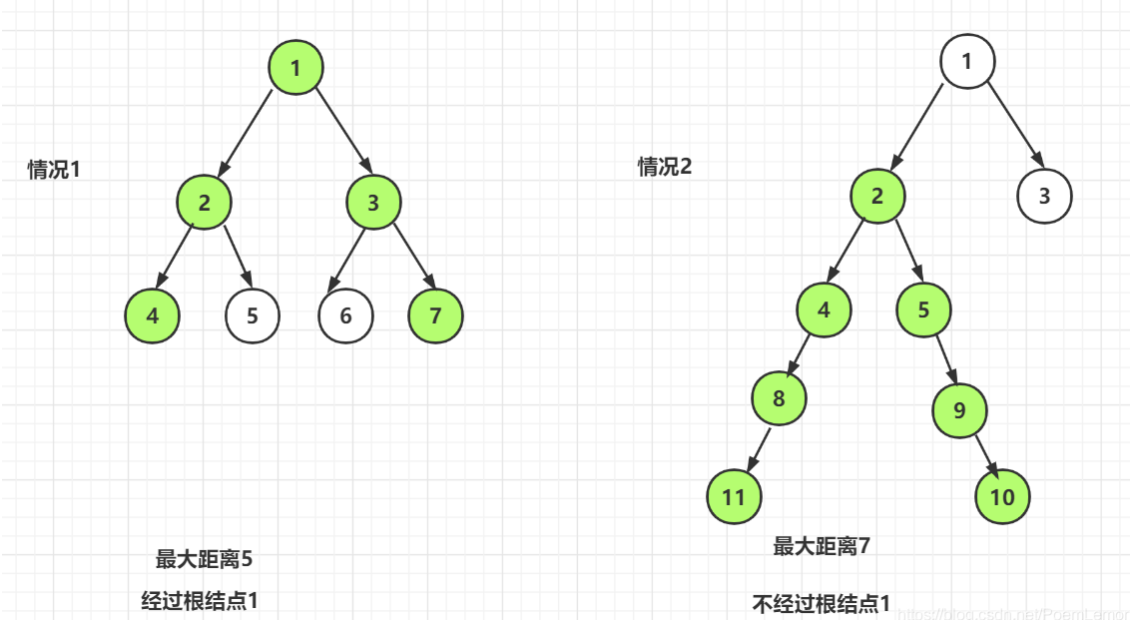
这棵树的最大距离（首先构建出这个模型，和高中的受力分析意义画出图来）：max(左子树的最大距离，右子树的最大距离，左子树的高度+右子树的高度+1)
子问题的解有重叠：f(n-1)是f(n)解的一部分，确定边界值为某个叶子节点的解为f(0)=max(0, 0, 1)=1。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
struct RetVal { // 涉及到两个变量，先定义结构体
    int distance;
    int height;
    RetVal(int dis, int hgt) : distance(dis), height(hgt) {}
};

int Do(TreeNode *root)
{
    if (root == nullptr) return 0;
    return dfs(root).distance;
}

// 后序遍历
RetVal dfs(TreeNode *root)
{
    if (root == nullptr) return RetVal(0, 0);
    RetVal left = dfs(root->left);
    RetVal right = dfs(root->right);
    int height = std::max(left.height, right.height) + 1; // 需要计算高度
    // 左子树的最大距离，右子树的最大距离，左子树的高度+右子树的高度+1
    return RetVal(std::max(std::max(left.distance, right.distance), left.height + right.height + 1), height);
}

翻转二叉树

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。


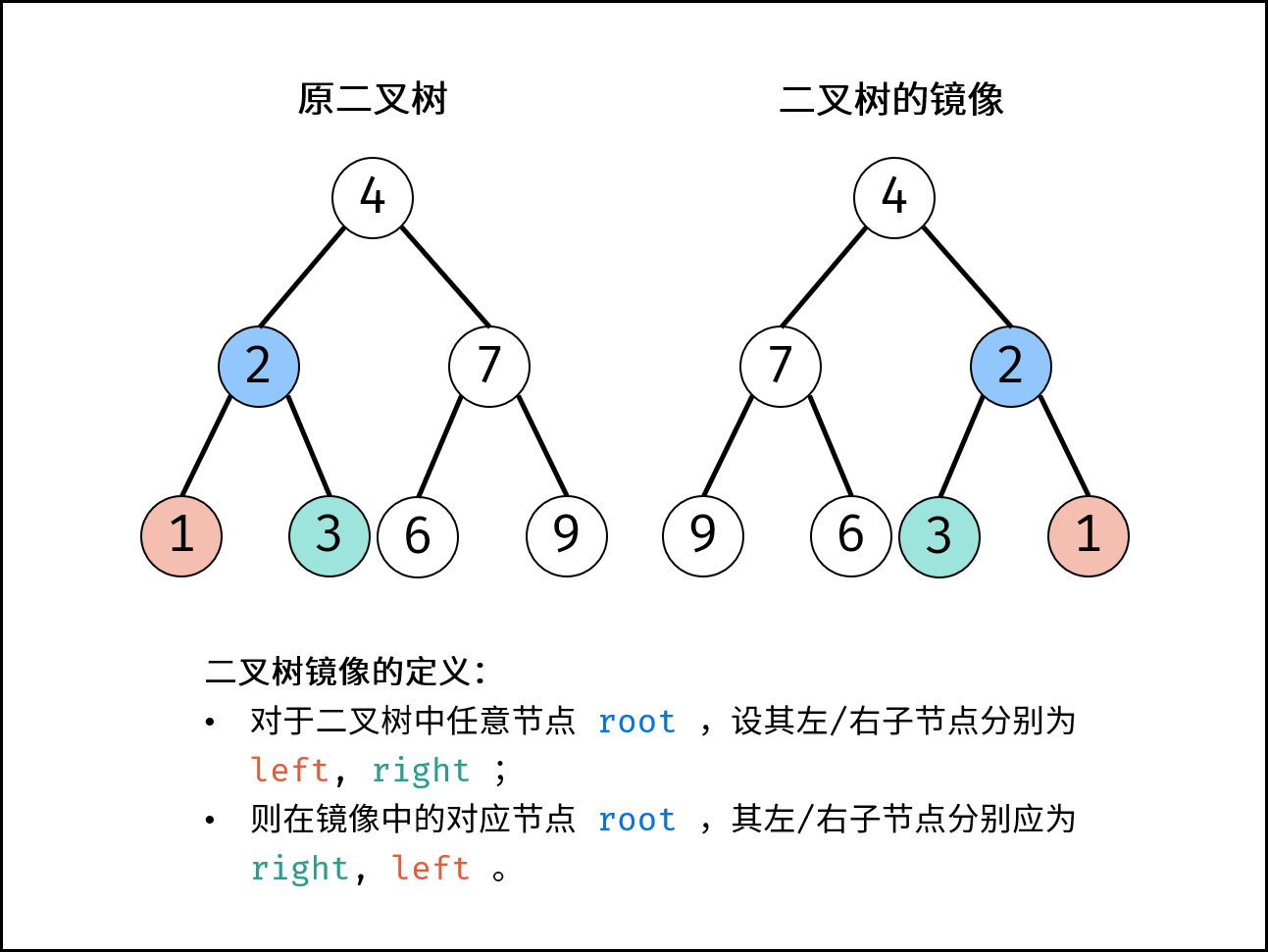
根据二叉树镜像的定义，考虑递归遍历（dfs）二叉树，交换每个节点的左 / 右子节点，即可生成二叉树的镜像。
Q： 为何需要暂存 root 的左子节点？
A： 在递归右子节点 “root.left=invertTree(root.right);” 执行完毕后， root.left 的值已经发生改变，此时递归左子节点 invertTree(root.left) 则会出问题。

1
2
3
4
5
6
7
TreeNode* invertTree(TreeNode* root) {
    if (root == nullptr) return nullptr;
    TreeNode* tmp = root->left;
    root->left = invertTree(root->right);
    root->right = invertTree(tmp);
    return root;
}

利用栈（或队列）遍历树的所有节点 nodenodenode ，并交换每个 nodenodenode 的左 / 右子节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
TreeNode* invertTree(TreeNode* root) {
    if (root == nullptr) return nullptr;
    stack<TreeNode*> stack;
    stack.push(root);
    while (!stack.empty())
    {
        TreeNode* node = stack.top();
        stack.pop();
        if (node->left != nullptr) stack.push(node->left);
        if (node->right != nullptr) stack.push(node->right);
        TreeNode* tmp = node->left;
        node->left = node->right;
        node->right = tmp;
    }
    return root;
}

二叉搜索树中的插入操作

给定二叉搜索树（BST）的根节点 root 和要插入树中的值 value ，将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ，新值和原始二叉搜索树中的任意节点值都不同。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果。

根据二叉搜索树的性质，可以巧妙的将待插入结点转变为叶子结点插入，从而避免改变二叉树原有整体结构。 原因：二叉树搜索树本身就是有序的，按照其有序性，遍历找到目标val位置，一定能找到空子树，即NULL，此时构建新节点，将val插入即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
// 递归
TreeNode* insertIntoBST(TreeNode* root, int val) {
    if(root == NULL) return new TreeNode(val);
    if(root->val > val) root->left = insertIntoBST(root->left, val);
    else root->right = insertIntoBST(root->right, val);
    return root;
}
// 迭代
TreeNode* insertIntoBST(TreeNode* root, int val) {
    if(root == NULL) return new TreeNode(val);
    TreeNode* cur = root;
    while (cur != NULL) {
        if (cur->val > val){
            if (cur->left == NULL){ 
                cur->left = new TreeNode(val);
                break;
            } else {
                cur = cur->left;
            }
        } else {
            if (cur->right == NULL) {
                cur->right = new TreeNode(val);
                break;
            } else {
                cur = cur->right;
            }
        }
    }
    return root;
}

二叉树最大深度？

给定一个二叉树 root ，返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
思路：
使用两个栈，一个用于存储节点，另一个用于存储节点的深度。我们从根节点开始，逐层遍历树的节点，同时记录每个节点的深度。最终，返回最大深度作为结果。这种方法避免了递归，减小了函数调用栈的开销。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
int maxDepth(TreeNode* root) {
    if (root == nullptr) {
        return 0;  // 如果根节点为空，返回深度0
    }

    // 使用DFS进行深度搜索
    std::stack<TreeNode*> nodes;
    std::stack<int> depths;
    int max = 0;

    nodes.push(root);
    depths.push(1);  // 根节点的深度为1

    while (!nodes.empty()) {
        TreeNode* node = nodes.top();
        nodes.pop();
        int depth = depths.top();
        depths.pop();
        max = std::max(max, depth);  // 更新最大深度

        // 遍历左子树
        if (node->left) {
            nodes.push(node->left);
            depths.push(depth + 1);  // 左子树深度加1
        }
        // 遍历右子树
        if (node->right) {
            nodes.push(node->right);
            depths.push(depth + 1);  // 右子树深度加1
        }
    }

    return max;  // 返回最大深度
}

nephen wechat
欢迎您扫一扫上面的微信公众号，订阅我的博客！
坚持原创技术分享，您的支持将鼓励我继续创作！